Propagator Networks in F#

Read Time: 17 minutes

Propagator Networks are an interesting approach to computation. Today I want to provide an introduction to the concept of propagators using F#.

First, what is a propagator network? In short, it is a computational method that provides a unique approach to model information and it’s flow through a system. It’s concepts and motivations are described in several papers by Alexey Radul and Gerald Sussman, references below. Here I’ll provide a brief overview as well as some examples. On the surface, propagator networks are constructed of two primary components: cells and propagators. Cells are independent entities that maintain their own data. Propagators are functional connectors that propagate information between cells. These two parts work together to provide a method of data accumulation and computation.

To go a bit deeper, cells don’t just hold data, but accumulate data. For datatypes like int, this is relatively straight-forward. When a cell is created it may have a known value. But it may also be unknown (no information), since the implementation uses the Option type, it initialized with None. As data is processed through the network, a cell may increase it’s information with an actual value when available. For an Interval datatype this is more interesting. It too can have information when initialized, but in cases where there is no information, it is initialized with None. But as the network processes data, the cell accumulates additional information, resulting in more accurate interval values.

Propagators calculate and push data through the network, allowing cells to accumulate additional information. Propagators must adhere to several rules. They must be monotonically increasing. The information they pass to a cell must be at least as good or better than what the cell contained before. Since a cell is an Option type, in a basic sense any value is better than None (information is better than no information). The real power is best seen using the Interval datatype. For example, if a cell has the value range 10.1 - 12.2, any value a propagator passes to that cell must be at least this good. A new value of 10.1 - 11.0 is more precise (better), but a value of 9.0 - 15.0 is less precise (worse). As a result, a propagator would update the cell with the former value, but not the latter. Propagators must also be idempotent. Since a propagator can be triggered to executed multiple times, it must return the same data. These attributes work to support stability, internal autonomy, asynchronous execution, as well as proper accumulation of information.

Propagators should also be bi-directional in their computational ability. This is what allows data to flow in both directions across operators. In general this means a propagator for the function p(a) = b should have bundled an equivalent function p'(b) = a. As an example, imagine a function a + b = c. There are reciprocal functions c - b = a and c - a = b. A propagator is the bundling of these functions together so that given any two values it can provide the third. This allows a developer to write adder a b c to create an addition function of a + b = c, but get functional computation in all directions for free.

These components and their associated rules provide some interesting computational characteristics for accumulating data. A model of data relationships only need to be defined once. It enables data population from diverse sources, and a more robust representation of knowledge. Also, those reading might think these concepts bear a striking resemblance to CRDT and join-semilattice, and they would be correct. This is a useful comparison to carry mentally when thinking about propagator networks.

Moving onto the code portion of the post, the below examples were created using .NET Core 3.1. As a caveat, this is an experimental project. I’m using it to research several concepts surrounding propagator networks. So it is functional, but not currently production ready. Beyond internal implementation choices I’m playing with the semantics and library ergonomics. As a result, the code you see below will certainly shift over time. This doesn’t change the underlying concepts of propagator networks. The library is available below. 

1
dotnet new package propagator --version 0.1.0

Temperature Conversion

I want to pull a couple examples from the previously mentioned papers to walk through the process. First is a temperature conversion example. The math on this is so simple that using propagators can feel like overkill, but the simplicity allows focus on the propagator mechanics without getting too caught up in complex formulas. Even with simple formulas, don’t underestimate the ability to define mathematical relationships once.

Building a propagator network is a multiple step process. Starting with the temperature conversion formula F = C * 1.8 + 32, there are several components and operations to be codified. But before getting into the details, a diagram assists in conceptualization of the entire formula and how the it is broken down.

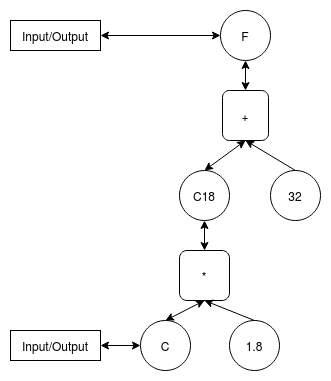
Temperature Converter

First, cells need to be created to hold data. There are the two end points (Celsius and Fahrenheit) that will serve as input or output, depending on conversion direction. There are also constants in the formula (1.8 and 32). Additionally, and perhaps less obvious at first glance, there are sub-results for the intermediate operations within the formula (C * 1.8). When the function is initially created the only values known are the ones sent in (C or F) and the constants. Beyond that, everything else is uninitialized.

Second, the relationships between the cells need to be defined, these are the propagators. Conveniently, the library has built-in propagators to support common math operations. A multiplier propagator will represent the C * 1.8 = C18 sub-component. An adder propagator will then take that sub-result and combine it for a final result C18 + 32 = F. These propagators are all that is needed to wire things together.

With the network in place, all that is needed now is to set the input and run the network. Since this is meant to work in either direction, it will accept and return both Celsius and Fahrenheit values. Below is the implementation.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/// TemperatureConverter
/// F = C * 1.8 + 32 
let temperatureConverter (c: float option) (f: float option) =
  let network = PropagatorNetwork()
  let cellc = network.AddCell c
  let cell18 = network.AddConstant 1.8
  let cellc18 = network.AddCell None
  let cell32 = network.AddConstant 32.
  let cellf = network.AddCell f
  
  multiplier cellc cell18 cellc18 |> network.AddPropagator
  adder cellc18 cell32 cellf |> network.AddPropagator

  network.Run()
  (network.GetFloat cellc, network.GetFloat cellf)

With the Celsius/Fahrenheit relationship defined, I can now call conversions in either direction.

1
2
3
4
5
6
7
8
9
10
11
12
13
// C -> F
match (temperatureConverter (Some 20.) None) with
| Some(c), Some(f) -> printfn "%5.2fc = %5.2ff" c f
| _ -> printfn "Conversion undetermined"

// F -> C
match (temperatureConverter None (Some 80.)) with
| Some(c), Some(f) -> printfn "%5.2fc = %5.2ff" c f
| _ -> printfn "Conversion undetermined"

// Results:
20.00c = 68.00f
26.67c = 80.00f

Just for kicks I can easily add capability. The propagator network can be expanded to support Kelvin. By adding a single propagator for a C = K - 273.15 conversion, the network now supports conversions between all three systems in any direction. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
let temperatureConverterCFK (c: float option) (f: float option) (k: float option) =
  let network = PropagatorNetwork()
  let cellc = network.AddCell c
  let cell18 = network.AddConstant 1.8
  let cellc18 = network.AddCell None
  let cell32 = network.AddConstant 32.
  let cellf = network.AddCell f
  let cellk = network.AddCell k
  let cell27315 = network.AddConstant 273.15

  // F = C × 1.8 + 32 
  multiplier cellc cell18 cellc18 |> network.AddPropagator
  adder cellc18 cell32 cellf |> network.AddPropagator
  // C = K - 273.15
  subtracter cellk cell27315 cellc |> network.AddPropagator

  network.Run()
  (network.GetFloat cellc, network.GetFloat cellf, network.GetFloat cellk)


// Kelvin conversions
[ (Some 20., None, None)
  (None, Some 80., None)
  (None, None, Some 200.) ]
|> List.iter(fun (c, f, k) ->
  match (temperatureConverterCFK c f k) with
  | Some(c), Some(f), Some(k) -> printfn "%6.2fc = %6.2ff = %6.2fk" c f k
  | _ -> printfn "Conversion undetermined")

// Results:
 20.00c =  68.00f = 293.15k
 26.67c =  80.00f = 299.82k
-73.15c = -99.67f = 200.00k

Estimating Building Height

Moving beyond relatively simple conversions, there are more complicated data relationships that can be represented using propagator networks. That leads to the second example, estimating the height of a building. It specifically addresses the idea of imperfect information and how multiple sources of truth can improve the overall quality of knowledge. Again, this is an example pulled from the reference papers. It isn’t exact clone though, I provide a slightly different twist to show additional dynamics.

For the resourceful person, there is more than one way to estimate the height of a building. Assuming I have a barometer at my disposal, I have encoded three possible methods below. First, I can drop an object from the top of the building and time how long it takes to hit the ground. The associated formula is height = 0.5 * g * t^2. Second, leveraging the knowledge of similar triangles, I can measure the height and shadow of a small object setting beside the building as well as the building’s shadow. The associated formula is buildingHeight / buildingShadow = smallHeight / smallShadow. Third, I can count the rows of windows and estimate the height of a floor. The associated formula is height = floors * floorHeight. These are all reasonable, but imprecise, estimation methods. We’ll also find that the total is better than the sum of all parts.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/// Height - using fall duration and shadow length and floor count
let buildingHeight (fallTime: Interval option) (buildingShadow: Interval option) (barometerHeight: Interval option) (barometerShadow: Interval option) (floors: Interval option) (floorHeight: Interval option) =
  let buildingHeight = None
  let network = PropagatorNetwork()

  // Height based on fall time
  // Fall duration: d = 0.5 * g * t^2
  let fallTime = network.AddCell fallTime
  let two = network.AddConstant { Interval.Min = Some 2.; Max = Some 2.}
  let t2 = network.AddCell None
  let g = network.AddConstant { Interval.Min = Some 9.80665; Max = Some 9.80665 }
  let gt2 = network.AddCell None
  let half = network.AddConstant { Interval.Min = Some 0.5; Max = Some 0.5 }
  let buildingHeight = network.AddCell buildingHeight
  
  power fallTime two t2 |> network.AddPropagator
  multiplier g t2 gt2 |> network.AddPropagator
  multiplier half gt2 buildingHeight |> network.AddPropagator

  // Shadow
  // Similar triangles Shadow Ratio = Height / Shadow
  let barometerHeight = network.AddCell barometerHeight
  let barometerShadow = network.AddCell barometerShadow
  let buildingShadow = network.AddCell buildingShadow
  let shadowRatio = network.AddCell None

  divider barometerHeight barometerShadow shadowRatio |> network.AddPropagator
  divider buildingHeight buildingShadow shadowRatio |> network.AddPropagator

  // Floors
  let floorCount = network.AddCell floors
  let floorHeight = network.AddCell floorHeight
  
  multiplier floorHeight floorCount buildingHeight |> network.AddPropagator

  network.Run()
  
  (network.GetInterval fallTime, network.GetInterval buildingHeight, network.GetInterval buildingShadow, network.GetInterval floorCount, network.GetInterval floorHeight)

/// Create an in interval type
let interval (min: float option) (max: float option) =
  Some { Interval.Min = min; Max = max }

One thing about imprecise measurements is the need for a datatype that supports values with a margin of error. Enter Interval, a built-in propagator library type. Instead of using float for building height estimates, Interval provides a range of possible values per each measurement method. This facilitates the storing of imperfect information.

In the first scenario, I have a barometer. I decide to drop the barometer from the top of the building and measure how long it takes to hit the ground. Frankly this feels like a destructive method of measurement, but desperate times… When measured, it takes about 4 seconds. But given that there is a natural delay when I start and stop the stopwatch, I assume I have a one second margin of error. This translates to a possible interval of between 3.5 and 4.5 seconds. With this knowledge I can feed that information in the buildingHeight function and find that the building is between 60 and 99 meters high. The function supports additional inputs, but since I don’t have additional information those parts of the propagator network are non-impacting.

1
2
3
4
5
6
let fallTime = interval (Some 3.5) (Some 4.5)
let (_, height', _, _, _) = buildingHeight fallTime None None None None None
printfn "Only fall time...                Height (m): %O" height'

// Result: 
Only fall time...                Height (m): Some([60.06573 .. 99.29233])

In the second scenario I use the knowledge of similar triangles and ratios. I can place the barometer on the ground beside the building and measure it’s shadow. Since the sun’s angle is similar for the barometer and building, I can use that information along with the length of the building’s shadow to gain an estimate of the building’s height. After some measurements it is determined that the barometer’s height and shadow are about 12.5cm and 24.5cm. The building’s shadow is about 170.5m long. Providing this additional information into the function I get a better estimate of the building’s height of between 81 and 92 meters high. It looks like I’m making progress.

1
2
3
4
5
6
7
8
let buildingShadow = interval (Some 170.0) (Some 171.0)
let barometerHeight = interval (Some 0.12) (Some 0.13)
let barometerShadow = interval (Some 0.24) (Some 0.25)
let (_, height', _, _, _) = buildingHeight fallTime buildingShadow barometerHeight barometerShadow None None 
printfn "Fall time and shadow...          Height (m): %O" height'

// Result: 
Fall time and shadow...          Height (m): Some([81.6 .. 92.625])

In the third scenario I can improve the estimate even more. I count the windows on the outside and determine it has 30 floors. I can also make an educated guess that each floor is about 3-3.5 meters high. Using this third piece of information I can enhance the building’s height estimate even more to 90 to 92 meters high. The power of multiple sources is magnified. Using three different sources, all with their own margin of error, I can easily aggregate the results to reduce the overall margin of error.

1
2
3
4
5
6
7
let floors = interval (Some 30.) (Some 30.)
let floorHeight = interval (Some 3.) (Some 3.5)
let (_, height', _, _, _) = buildingHeight fallTime buildingShadow barometerHeight barometerShadow floors floorHeight
printfn "Fall time, shadow, and floors... Height (m): %O" height'

// Result:
Fall time, shadow, and floors... Height (m): Some([90 .. 92.625])

Stepping back, it helps to visualize in more detail how these intervals work together. Below are the results of each piece of knowledge by itself. They all have varying amounts of accuracy, but as additional information is added to the model, the final estimate is improved. 

1
2
3
4
5
6
7
// Separate results:
Only fall time...                Height (m): Some([60.06573 .. 99.29233])
Only shadow...                   Height (m): Some([81.6 .. 92.625])
Only floors...                   Height (m): Some([90 .. 105])

// Aggregated result:
Fall time, shadow, and floors... Height (m): Some([90 .. 92.625])

Aggregated Intervals

As a side note, this model contains the same type of dynamic relationships as the temperature conversion model. Data flows in all directions. Lets say for example I don’t feel good about a mental estimate of floor height, but I can still count windows. If I run the function and exclude my floorHeight measurement, I won’t get a better building height estimate, but I can get an additional estimate that the floor height is between 2.7 and 3.1 meters. With respect to knowledge aggregation, this is a nice attribute of propagator network models.

1
2
3
4
5
6
7
let (_, height', _, _, floorHeight') = buildingHeight fallTime buildingShadow barometerHeight barometerShadow floors None
printfn "Building Height (m): %O" height'
printfn "Floor Height (m)   : %O" floorHeight'

// Result:
Building Height (m): Some([81.6 .. 92.625])
Floor Height (m)   : Some([2.72 .. 3.0875])

These two examples provide some insight into the dynamics of propagator networks. I could go on, but I think this is a good break point. As an introduction to the concept of propagator networks, I hope you’ve found this computation approach interesting. If you want to dig in a bit more, additional references are below. Until next time.

References

Related Posts: